Bài tập ôn tập kiến thức môn Toán 9 - Tuần 22

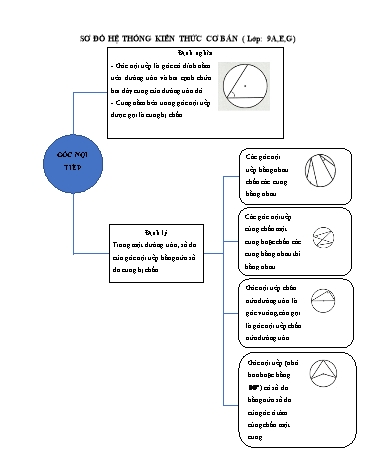
SƠ ĐỒ HỆ THỐNG KIẾN THỨC CƠ BẢN ( Lớp: 9A,E,G)GÓC NỘI TIẾP
Định nghĩa
- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
- Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn.
Định lý
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị chắn.
Các góc nội tiếp bằng nhau chắn các cung bằng nhau.


Các góc nội tiếp 
cùng chắn một 
cung hoặc chắn các cung bằng nhau thì bằng nhau.
 

Góc nội tiếp chắn nửa đường tròn là góc vuông, còn gọi là góc nội tiếp chắn nửa đường tròn.


Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.


Bài 1. Cho và điểm I nằm ngoài đường tròn. Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D). Chứng minh rằng .
Bài 2. Cho tam giác nhọn ABC nội tiếp đường tròn tâm O đường kính AM. Hạ AK vuông góc với BC .
a) Tính .
b) Gọi N là giao điểm của AK với đường tròn . Tứ giác BCMN là hình gì? Vì sao?
Bài 3. Cho tam giác nhọn ABC có . Vẽ đường tròn đường kính AC có tâm O, đường tròn này cắt BA và BC tại D và E.
a) Chứng minh .
b) Gọi H là giao điểm của CD và AE. Chứng minh rằng đường trung trực của đoạn HE đi qua trung điểm I của BH.
c) Chứng minh .
Bài 4. Cho nửa đường tròn đường kính AB. Kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đưởng tròn. Các tia AC và AD cắt Bx lần lượt ở E, F (F ở giữa B và E).
a) Chứng minh tích không đổi.
b) Chứng minh .
Bài 5. Cho đường tròn tâm O đường kính AB và điểm M bất kì trên nửa đường tròn sao cho . Gọi là điểm đối xứng của M qua AB và S là giao điểm của hai tia BM; . Gọi K là chân đường vuông góc từ S đến AB, là giao điểm của MA và SK.
a) Chứng minh là tam giác cân.
b) Chứng minh KM là tiếp tuyến của đường tròn.
Bài 6. Cho . Cạnh AB, BC, CA tiếp xúc với đường tròn tại các điểm D, E, F, BF cắt tại I, DI cắt BC tại M. Chứng minh
a) Tam giác DEF có ba góc nhọn.
b) .
c) .
Bài 7. Cho đường tròn bán kính R có hai đường kính AB và CD vuông góc với nhau. Trên đoạn thẳng AB lấy điểm M (M khác O), CM cắt tại N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở P.
a) Chứng minh tích không phụ thuộc vào vị trí của điểm M.
b) Khi M di chuyển trên đoạn thẳng AB thì P chạy trên đoạn thẳng cố định nào?